In the vast landscape of mathematics, there exists a powerful branch that holds the key to understanding the intricate relationships between angles and sides. Welcome to the world of trigonometry, where triangles become the building blocks for unraveling the mysteries of the universe. Trigonometry, derived from the Greek words "trigonon" (triangle) and "metron" (measure), serves as a mathematical toolkit essential for countless scientific and engineering applications.
Mastering Trigonometry A Comprehensive Guide with CBSE NCERT Download for a Solid Foundation
Trigonometric Ratios
Opposite & Adjacent Sides in a Right-Angled Triangle
In the ΔABC right-angled at B, BC is the side opposite to ∠A, AC is the hypotenuse, and AB is the side adjacent to ∠A.
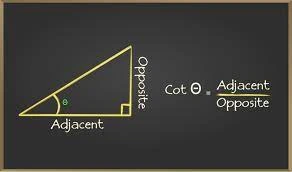
Trigonometric Ratios
For the right ΔABC, right-angled at ∠B, the trigonometric ratios of the ∠A are as follows:
- sin A=opposite side/hypotenuse=BC/AC
- cos A=adjacent side/hypotenuse=AB/AC
- tan A=opposite side/adjacent side=BC/AB
- cosec A=hypotenuse/opposite side=AC/BC
- sec A=hypotenuse/adjacent side=AC/AB
- cot A=adjacent side/opposite side=AB/BC
Relation between Trigonometric Ratios
-
cosec θ =1/sin θ
-
sec θ = 1/cos θ
-
tan θ = sin θ/cos θ
-
cot θ = cos θ/sin θ=1/tan θ

Visualization of Trigonometric Ratios Using a Unit Circle
Draw a circle of the unit radius with the origin as the center. Consider a line segment OP joining a point P on the circle to the center, which makes an angle θ with the x-axis. Draw a perpendicular from P to the x-axis to cut it at Q.
-
sin θ=PQ/OP=PQ/1=PQ
-
cos θ=OQ/OP=OQ/1=OQ
-
tan θ=PQ/OQ=sin θ/cos θ
-
cosec θ=OP/PQ=1/PQ
-
sec θ=OP/OQ=1/OQ
-
cot θ=OQ/PQ=cos θ/sin θ
Trigonometric Ratios of Specific Angles
The specific angles that are defined for trigonometric ratios are 0°, 30°, 45°, 60° and 90°.
Trigonometric Ratios of 45°
If one of the angles of a right-angled triangle is 45°, then another angle will also be equal to 45°.
Let us say ABC is a right-angled triangle at B, such that;
∠ A = ∠ C = 45°
Thus, BC = AB = a (say)
Using Pythagoras theorem, we have;
AC2 = AB2 + BC2
= a2 + a2
= 2a2
AC = a√2
CBSE Class 10 NCERT Mathematics Topics for a Strong Foundation (NCERT DOWNLOAD)
| Chapter Name | Introduction to Trigonometry |
| Topic Number | Topics |
| 8.1 | Introduction |
| 8.2 | Trigonometric Ratios |
| 8.3 | Trigonometric Ratios of Some Specific Angles |
| 8.4 | Trigonometric Identities |
| 8.5 | Summary |
Now, from the trigonometric ratios, we have
- sin 45° = (Opp. side to angle 45°)/Hypotenuse = BC/AC = a/a√2 = 1/√2
- cos 45° = (Adj. side to angle 45°)/Hypotenuse = AB/AC = a/a√2 = 1/√2
- tan 45° = BC/AB = a/a = 1
Similarly
- cosec 45° = 1/sin 45° = √2
- sec 45° = 1/cos 45° = √2
- cot 45° = 1/tan 45° = 1
The Historical Tapestry
Trigonometry's roots stretch far back in time, intertwining with the great civilizations of antiquity. Ancient astronomers, such as the Greeks and Indians, were among the first to recognize the significance of angles in the cosmos. From measuring the heights of towering pyramids to predicting celestial events, trigonometry became an indispensable tool for understanding the physical world.
The Language of Triangles
At its core, trigonometry revolves around the study of triangles. Whether you're dealing with right-angled triangles or more complex configurations, trigonometric functions like sine, cosine, and tangent emerge as the fundamental building blocks. These functions form the backbone of trigonometry, allowing us to relate the angles of a triangle to the lengths of its sides.
Range of Trigonometric Ratios from 0 to 90 Degrees
For 0∘≤θ≤90∘,
-
0 ≤ sin θ ≤ 1
-
0 ≤ cos θ ≤ 1
-
0 ≤ tan θ < ∞
1 ≤ sec θ < ∞ -
0 ≤ cot θ < ∞
-
1 ≤ cosec θ < ∞
tan θ and sec θ are not defined at 90∘.
cot θ and cosec θ are not defined at 0∘.
CBSE Class 10 Board Exam Sample Paper

[Previous Year Question Solution Maths Download Button]
[Previous Year Question Solution Science Download Button]
| CBSE CLASS 10 Mathematics Chapters |
| Chapter1: Real Numbers |
| Chapter2: Polynomials |
| Chapter3: Pair of Linear Equations in Two Variables |
| Chapter4: Quadratic Equations |
| Chapter5: Arithmetic Progressions |
| Chapter6: Triangles |
| Chapter7: Coordinate Geometry |
| Chapter8: Introduction to Trigonometry |
| Chapter9: Some Applications of Trigonometry |
| Chapter10: Circles |
| Chapter11: Areas Related to Circles |
| Chapter12: Surface Areas and Volumes |
| Chapter13: Statistics |
| Chapter14: Probability |
| CBSE CLASS 10 Science Chapters |
| Chapter1: Chemical Reactions and Equations |
| Chapter2: Acids, Bases and Salts |
| Chapter3: Metals and Non-metals |
| Chapter4: Carbon and its Compounds |
| Chapter5: Life Processes |
| Chapter6: Control and Coordination |
| Chapter7: How do Organisms Reproduce? |
| Chapter8: Heredity |
| Chapter9: Light – Reflection and Refraction |
| Chapter10: The Human Eye and the Colourful World |
| Chapter11: Electricity |
| Chapter12: Magnetic Effects of Electric Current |
| Chapter13: Our Environment |
| Class 8 |
| Class 9 |
| Class 11 |
| Class 12 |
CBSE Class 10th Downloadable Resources:
| 1. CBSE Class 10th Topic Wise Summary | View Page / Download |
| 2. CBSE Class 10th NCERT Books | View Page / Download |
| 3. CBSE Class 10th NCERT Solutions | View Page / Download |
| 4. CBSE Class 10th Exemplar | View Page / Download |
| 5. CBSE Class 10th Previous Year Papers | View Page / Download |
| 6. CBSE Class 10th Sample Papers | View Page / Download |
| 7. CBSE Class 10th Question Bank | View Page / Download |
| 8. CBSE Class 10th Topic Wise Revision Notes | View Page / Download |
| 9. CBSE Class 10th Last Minutes Preparation Resources (LMP) | View Page / Download |
| 10. CBSE Class 10th Best Reference Books | View Page / Download |
| 11. CBSE Class 10th Formula Booklet | View Page / Download |
Being in CBSE class 10th and considering the board examinations you must be needing resources to excel in your examinations. At TestprepKart we take great pride in providing CBSE class 10th all study resources in downloadable form for you to keep you going.
Below is the list of all CBSE class 10th Downloads available on TestprepKart for both Indian and NRI students preparing for CBSE class 10th in UAE, Oman, Qatar, Kuwait & Bahrain.
FAQ
Q1. What is Trigonometry?
Ans Trigonometry is a branch of mathematics that focuses on the relationships between the angles and sides of triangles. It explores the properties of these geometric elements and provides a set of functions to analyze and solve problems involving angles and distances.
Q2. Why is Trigonometry Important?
Ans Trigonometry is essential in various fields, such as physics, engineering, architecture, and astronomy. It helps in measuring distances, analyzing forces, designing structures, and understanding the behavior of waves and oscillations.
Q3. What are the Basic Trigonometric Functions?
Ans The fundamental trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions relate the angles of a triangle to the lengths of its sides and are crucial in solving trigonometric equations and applications.
Q4. How is Trigonometry Used in Real Life?
Ans Trigonometry has numerous real-world applications. It is used in navigation for calculating distances and directions, in physics to analyze waves and oscillations, and in architecture and engineering for designing structures and determining forces.
Q5. Can Trigonometry be Fun to Learn?
Ans Absolutely! Trigonometry might seem challenging at first, but many find it enjoyable once they grasp its concepts. Practical applications and hands-on problem-solving can make learning trigonometry a rewarding and engaging experience.
Leave a Reply