In the rich tapestry of vector mathematics, the cross-product emerges as a fascinating and powerful operation, revealing the intricate relationships between vectors in three-dimensional space. This mathematical tool, represented by the symbol "×," holds the key to understanding the geometric nuances that govern vectors' behaviour. As we embark on this exploration, let's delve into the essence, applications, and significance of the cross-product.
Cross Product of Two Vectors
Cross-product is a form of vector multiplication, performed between two vectors of different natures or kinds. A vector has both magnitude and direction. We can multiply two or more vectors by cross product and dot product. When two vectors are multiplied with each other and the product of the vectors is also a vector quantity, then the resultant vector is called the cross product of two vectors or the vector product. The resultant vector is perpendicular to the plane containing the two given vectors.
Cross Product Definition
If A and B are two independent vectors, then the result of the cross product of these two vectors (Ax B) is perpendicular to both the vectors and normal to the plane that contains both the vectors. It is represented by:
A x B= |A| |B| sin θ
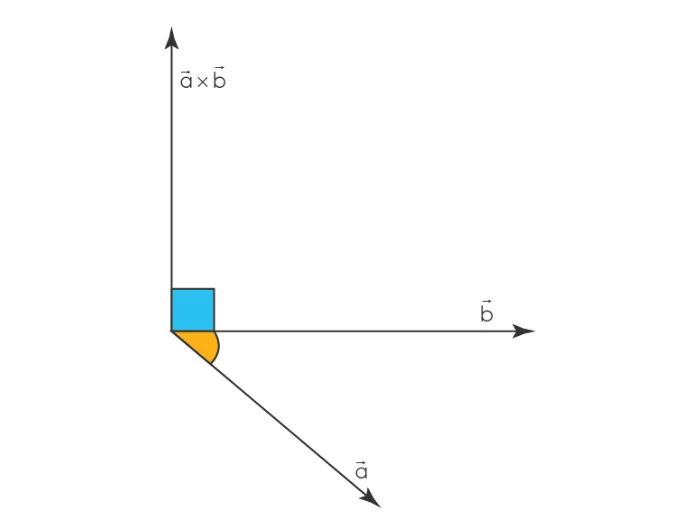
We can understand this with an example that if we have two vectors lying in the X-Y plane, then their cross product will give a resultant vector in the direction of the Z-axis, which is perpendicular to the XY plane. The × symbol is used between the original vectors. The vector product or the cross product of two vectors is shown as:
→a→×b→=c→
Where
A→ And b→ are two vectors.
C → is the resultant vector.
Cross Product of Two Vectors Meaning
The cross product of two vectors is a mathematical operation with profound implications, offering valuable insights into vector algebra and geometric relationships. Let's unravel the meaning and significance encapsulated within the cross product, exploring its fundamental attributes and practical applications.
Foundational Essence:
At its essence, the cross product is a vector operation denoted as A×B, where A and B are the input vectors. The outcome is a vector that stands perpendicular to the plane formed by the original vectors.
Directionality and Orthogonality:
One of the most distinctive features of the cross product is its ability to yield a vector that is orthogonal to both input vectors. This characteristic becomes a powerful tool for determining spatial orientations, as the resulting vector is orthogonal to the plane defined by the original vectors.
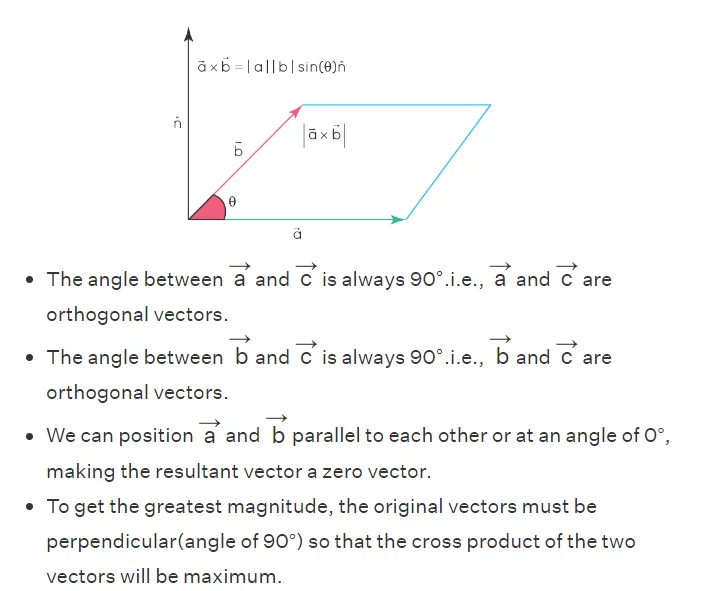
Geometric Interpretation:
Visualising the cross product reveals a geometric interpretation. The magnitude of the cross product corresponds to the area of the parallelogram formed by the two vectors. This geometric perspective underscores its role in quantifying spatial relationships.
Cross Product Formula
The resulting vector A×B has three components: one for each dimension (x, y, and z). The components are calculated using the determinants of 2×2 matrices formed by the components of the original vectors. The order in which you perform the calculations matters, as it determines the direction of the resulting vector.
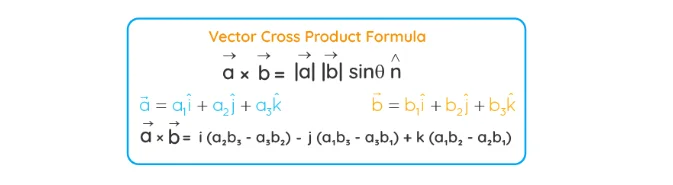
Right-Hand Rule – Cross Product of Two Vectors
The right-hand rule is a convention used to determine the direction of the resulting vector when taking the cross product of two vectors. The rule is applied as follows:
Orientation of the Hand:
-
Extend your index finger in the direction of the first vector (A).
-
Extend your middle finger in the direction of the second vector (B).
Resultant Direction:
-
Your thumb, when extended perpendicular to the plane formed by your index and middle fingers, points in the direction of the resulting vector (A×B).
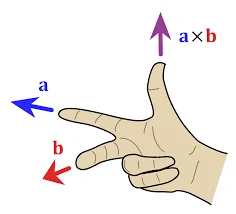
This rule provides a consistent way to determine the direction of the cross product. It's important to note that the order of vectors matters. If you switch the order of the vectors in the cross product (B×A), the direction of the resulting vector will be opposite; you would use the left-hand rule instead.

Cross Product of Two Vectors Example
Cross product plays a crucial role in several branches of science and engineering. Two very basic examples are shown below.
Example 1: Turning on the tap: We apply equal and opposite forces at the two diametrically opposite ends of the tap. Torque is applied in this case. In vector form, torque is the cross product of the radius vector (from the axis of rotation to the point of application of force) and the force vector.
i.e.
→T→=R→×F→

Example 2: Twisting a bolt with a spanner: The length of the spanner is one vector. Here the direction we apply force on the spanner (to fasten or loosen the bolt) is another vector. The resultant twist direction is perpendicular to both vectors.
Important Notes
-
The cross product of two vectors results in a vector that is orthogonal to the two given vectors.
-
The direction of the cross product of two vectors is given by the right-hand thumb rule and the magnitude is given by the area of the parallelogram formed by the original two vectors →a→ and →b→.
-
The cross-product of two linear vectors or parallel vectors is a zero vector.
SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES:
Q1: What is the vector product of two vectors?
A: The vector product, also known as the cross product, is a mathematical operation between two vectors in three-dimensional space. It results in a vector that is perpendicular to the plane formed by the original vectors.
Q2: How is the cross product calculated?
A: For two vectors [answer image ]
Q3: What is the geometric interpretation of the cross product?
A: Geometrically, the cross product produces a vector that is perpendicular to the plane formed by the original vectors. Its magnitude is equal to the area of the parallelogram formed by the vectors.
Q4: How is the right-hand rule used in the cross product?
A: The right-hand rule is a convention used to determine the direction of the resulting vector. If you point your index finger in the direction of the first vector, your middle finger in the direction of the second vector, then your thumb points in the direction of the cross product.
Q5: What is the significance of the cross product in physics and engineering?
A: The cross product has various applications, including determining torque, finding the direction of angular momentum, and generating normal vectors for surfaces in physics, engineering, and computer graphics.

Leave a Reply