Understanding the dynamics of motion involves exploring the fascinating relationship between angular velocity and linear velocity. In this blog, we'll delve into the intricacies of these two essential concepts, unravelling their connection and shedding light on their significance in the world of physics.
Angular velocity and its relation with linear velocity
ANGULAR VELOCITY
Angular velocity is a measure of how quickly an object rotates or revolves around a specific point or axis. It represents the rate of change of angular displacement with respect to time. The angular displacement is the angle through which an object rotates in a given time period.

Angular velocity is typically denoted by the Greek letter ω (omega). Mathematically, it is defined as:
w=ΔtΔ0
where:
ω is the angular velocity,
Δθ is the change in angular displacement,
Δt is the change in time.
The SI unit for angular velocity is radians per second (rad/s). Alternatively, degrees per second (°/s) can be used, but radians per second are more commonly employed in scientific and engineering contexts.
Formula of Angular Velocity

Types of Angular velocity
Angular velocity can be classified into two main types: average angular velocity and instantaneous angular velocity.
Average Angular Velocity:
Formula:
Average Angular Velocity(wˉ)=ΔtΔ0
Description: The average angular velocity is the change in angular displacement (Δθ) divided by the corresponding change in time (Δt). It provides an average rate of rotation over a given time interval.
Instantaneous Angular Velocity:
Formula:
Instantaneous Angular Velocity(w)=limΔt→0ΔtΔ0
Description: The instantaneous angular velocity is the limit of the average angular velocity as the time interval (Δt) approaches zero. In other words, it represents the angular velocity at a specific instant in time. It is often denoted simply as ω.
Both average and instantaneous angular velocities are measured in units of radians per second (rad/s) or degrees per second (°/s), depending on the angular displacement units used.
Additionally, angular velocity can have different directions:
Positive Angular Velocity: When an object rotates counterclockwise, the angular velocity is considered positive.
Negative Angular Velocity: When an object rotates clockwise, the angular velocity is considered negative.
example of Angular Velocity:

Linear Velocity
Linear velocity is the rate of change of an object's position in a straight line per unit of time. In other words, it measures how quickly an object is moving along a straight path. Linear velocity is a vector quantity, meaning it has both magnitude and direction.
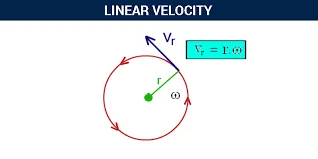
The formula for linear velocity (v) is given by:
v=ΔtΔs
Where:
v is the linear velocity, Δs is the change in position or displacement of the object, Δt is the change in time.
The SI unit for linear velocity is metres per second (m/s), but it can also be expressed in other units such as kilometres per hour (km/h) or miles per hour (mph), depending on the specific context.
Linear velocity is closely related to speed, which is the magnitude of velocity without considering direction. However, linear velocity includes both the speed and the direction of motion, making it a more comprehensive measure of an object's movement along a straight path.

Types of Linear Velocity
Tangential Velocity:
Definition: The linear velocity of an object moving along a circular path. It represents the speed and direction of an object's motion at any point on the circumference of the circle.
Formula: Vt = ω⋅r, where is the tangential velocity, ω is the angular velocity, and r is the radius of the circular path.
Radial Velocity:
Definition: The linear velocity of an object moving along a radial line (straight line from the centre) in a circular path. Radial velocity is perpendicular to the tangential velocity and changes as the object moves around the circle.
Formula: Radial velocity is not constant unless the object is moving in a perfect circle.
Constant Linear Velocity:
Definition: When an object moves in a straight line with a constant speed and direction, its linear velocity is constant. This is typical for objects undergoing uniform linear motion.
Formula: v=ΔtΔs , where v is the constant linear velocity, Δs is the displacement, and Δt is the time interval.
Variable Linear Velocity:
Definition: In cases where an object's speed or direction changes, the linear velocity is considered variable. This can occur in non-uniform linear motion or when an object is subject to acceleration or deceleration.
Formula: The general formula v=ΔtΔs is used, but the velocity may vary at different points in time.
SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES:
Q1 What is Angular Velocity?
Answer: Angular velocity is the rate at which an object rotates about an axis. It measures how quickly an object is spinning and is typically denoted by the symbol ω.
Q2 How is Angular Velocity Calculated?
Answer: Angular velocity (ω) is calculated as the change in angular displacement (Δθ) divided by the change in time (Δt): W=ΔYΔX
Q3 What is Linear Velocity?
Answer: Linear velocity (v) is the rate of change of an object's position in a straight line per unit of time. It measures how quickly an object is moving along a straight path.
Q4 How are Angular and Linear Velocities Related?
Answer: The relationship between angular velocity (ω) and linear velocity (v) is given by the formula v=ω⋅r, r is the radius of the circular path.
Q5 Can Angular Velocity Exist Without Linear Velocity?
Answer: Yes, angular velocity can exist without linear velocity if an object is rotating about an axis without translating in a straight line. However, when linear motion is involved, there is a connection between angular and linear velocities.

Leave a Reply