In the realm of rotational dynamics, the concepts of torque and angular momentum play pivotal roles in unveiling the complexities of objects in motion. Torque, akin to force in linear motion, governs the rotational forces that lead to spinning or twisting motion. On the other hand, angular momentum encapsulates the quantity of rotational motion possessed by an object, amalgamating its angular speed and resistance to changes in rotation. This introduction delves into the fundamentals of torque and angular momentum, shedding light on their definitions, significance, and the intricate interplay within the dynamic world of rotational physics.
Navigating Rotational Dynamics: Unveiling the Forces of Torque and the Spirals of Angular Momentum.
Torque Momentum
Torque is the measure of the tendency of a force to rotate an object around an axis or pivot point. It quantifies the effectiveness of a force in causing an object to rotate. Torque is a rotational counterpart to force in linear motion.

Formula:
The torque (τ) acting on an object is calculated using the formula:
τ=r×F
Where r is the lever arm (distance from the axis of rotation to the point where the force is applied), and F is the applied force.
Units:
Torque is measured in newton-metres (N·m) in the International System of Units (SI) or foot-pounds (ft·lb) in the U.S. customary system.
Direction:
Torque is a vector quantity with both magnitude and direction. The direction of torque is determined by the right-hand rule: if you point your fingers in the direction of the force and curl them towards the direction of rotation, your thumb points in the direction of the torque.
Role in Rotational Motion:
Torque causes angular acceleration in a rotational system.
It is responsible for changing the angular velocity of an object.
Examples:
-
Turning a wrench.
-
Opening a door.
-
Spinning a wheel.
Certainly! Here are some topics related to "System of Particles and Rotational Dynamics" that you might find interesting:
Center of Mass:
Definition and calculation of the centre of mass for a system of particles.
Rotational Kinematics:
Describing rotational motion using angular displacement, angular velocity, and angular acceleration.
Moment of Inertia:
Understanding the concept of moment of inertia and its role in rotational motion.
Torque and Equilibrium:
Exploring the conditions for rotational equilibrium and the role of torque.
Angular Momentum Conservation:
Discussing the conservation of angular momentum and its applications.
Mathematical Expression of the Torque
The mathematical expression for torque (τ) is given by:
τ=r×F
Where: τ is the torque, r is the lever arm or the perpendicular distance from the axis of rotation to the point where the force is applied, F is the applied force.
This formula reflects the cross-product nature of torque, where the torque vector is the cross product of the position vector (r) and the force vector (F):
τ=r×F
In scalar form, for simplicity when dealing with magnitudes and not direction, the formula is:
τ=r⋅F⋅sin(θ)
Where: θ is the angle between the position vector and the force vector.


Angular momentum
Angular momentum is a fundamental concept in physics that quantifies the amount of rotational motion possessed by an object. It is the rotational analog of linear momentum and is crucial in describing the behaviour of rotating systems.
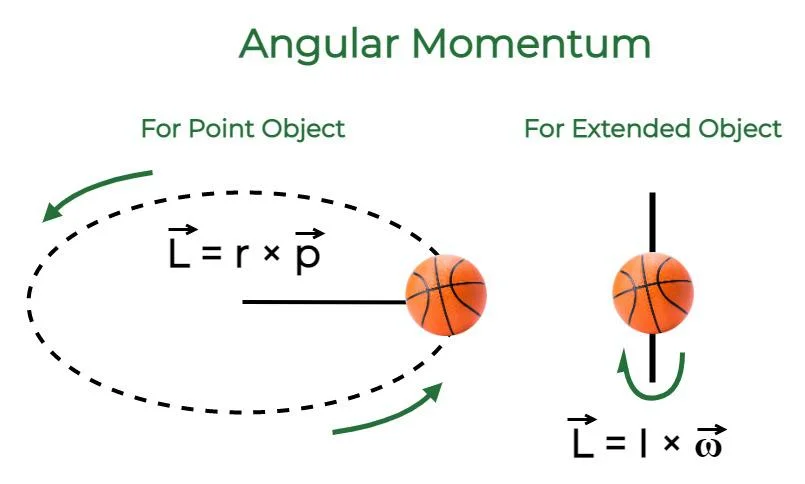
Mathematical Expression:
The formula for angular momentum (L) is given by the product of the moment of inertia (I) and the angular velocity (ω) of an object:
L=I⋅ω
where:
-
L is the angular momentum, I is the moment of inertia (a measure of an object's resistance to changes in rotation), ω is the angular velocity.
Conservation of Angular Momentum:
Angular momentum is conserved in the absence of external torques. This principle explains phenomena like the spinning motion of ice skaters pulling in their arms, resulting in an increase in angular velocity while conserving angular momentum.
Direction:
Angular momentum is a vector quantity, and its direction is determined by the right-hand rule. If you curl the fingers of your right hand in the direction of rotation, your thumb points in the direction of angular momentum.
Units:
The SI unit of angular momentum is kilogram-metre squared per second (kg·m²/s).
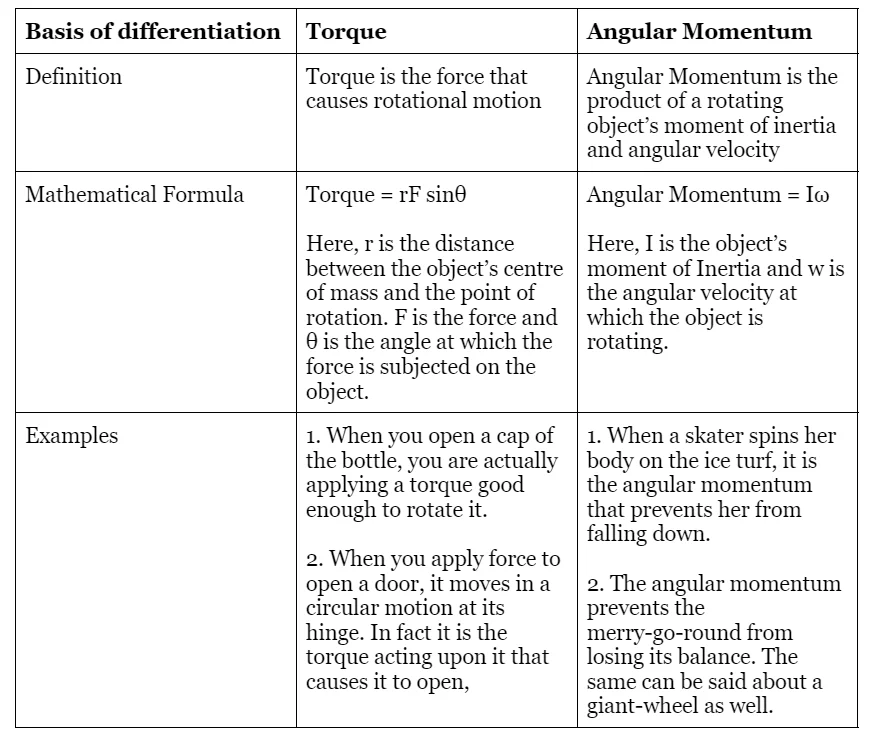
Difference between Torque & Angular momentum
SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES:
Q1 What is Torque?
Answer: Torque is the measure of the tendency of a force to rotate an object around an axis or pivot point. It is the rotational analog of force in linear motion.
Q2 How is Torque Calculated?
Answer: Torque (τ) is calculated using the formula τ=r×F, where r is the lever arm or distance from the axis, and F is the applied force.
Q3 What Factors Affect Torque?
Answer: Torque depends on the magnitude of the applied force, the lever arm's length, and the angle between the force and the lever arm.
Q4 How Does Torque Affect Rotational Motion?
Answer: Torque causes angular acceleration and is responsible for changing the angular velocity of an object in rotational motion.
Q5 What is Angular Momentum?
Answer: Angular momentum (L) is the quantity of rotational motion possessed by an object. It is calculated as the product of the moment of inertia and angular velocity:
L=I⋅ω.
Leave a Reply