Rotational motion, the dance of objects around a fixed axis, reveals a fascinating world of dynamics governed by angular displacement, velocity, and acceleration. In this blog, we will embark on a journey into the intricate realm of the kinematics of rotational motion about a fixed axis, unravelling the principles that govern the rotation of objects.
Unveiling the Intricacies of Kinematics in Rotational Motion about a Fixed Axis:
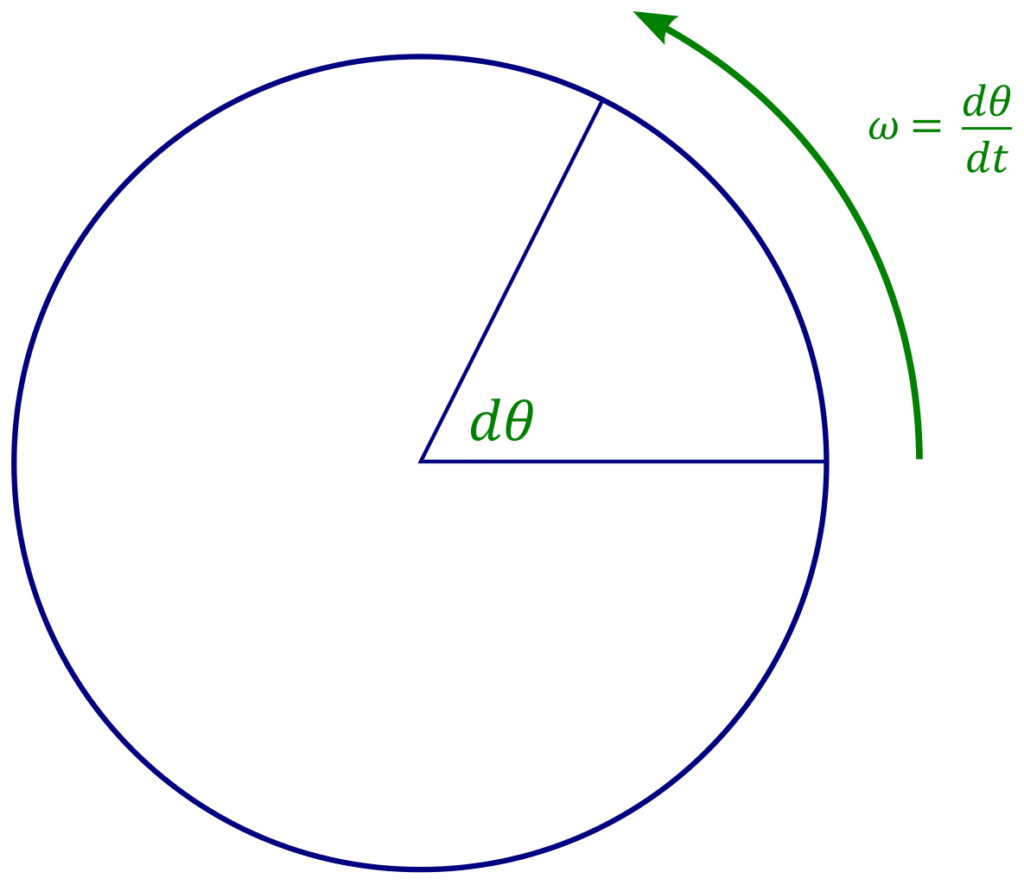
Angular Velocity:
Angular velocity (ω) is defined as the change in angular displacement (θ) with respect to time (t). Mathematically, it is expressed as:
w=ΔtΔ0
Here, ω represents angular velocity, Δθ is the change in angular displacement, and Δt is the corresponding time interval. Angular velocity is measured in radians per second (rad/s).
Directional Significance:
Angular velocity is a vector quantity, meaning it has both magnitude and direction. The direction is determined by the sign of the angular velocity. A positive angular velocity indicates counterclockwise rotation, while a negative angular velocity signifies clockwise rotation. This directional information is crucial for understanding the rotational dynamics of an object.
Connection with Linear Velocity:
There exists a close relationship between angular velocity and linear velocity (v), especially when considering objects in circular motion. The formula v=r⋅ω relates linear velocity to angular velocity, where r is the distance from the axis of rotation to the point of interest. This equation demonstrates how the linear and angular aspects of motion are interconnected.
Real-world Applications:
Angular velocity has widespread applications in various fields, including engineering, physics, and technology. In the context of machinery, such as the rotating components of engines, understanding angular velocity is crucial for optimising performance and efficiency. Wind turbines, gears, wheels, and flywheels are just a few examples where the principles of angular velocity are applied.
Angular Acceleration:
Angular acceleration (α) is a measure of how rapidly an object's angular velocity changes. Mathematically, it is defined as the rate of change of angular velocity with respect to time:
a=ΔtΔw
Here, α represents angular acceleration, Δω is the change in angular velocity, and Δt is the corresponding time interval. Angular acceleration is measured in radians per second squared (rad/s2).

Connection with Angular Velocity:
Angular acceleration is closely tied to angular velocity (ω). While angular velocity signifies how fast an object is rotating, angular acceleration tells us how quickly that rotation is changing. The relationship is encapsulated in the equation:
a=ΔtΔw
Understanding angular acceleration is crucial in scenarios where the rotation of an object is not constant or experiences changes over time.
Significance in Rotational Dynamics:
Angular acceleration plays a pivotal role in describing the dynamics of rotational motion. It accounts for variations in rotational speed and is instrumental in analysing the forces and torques acting on rotating objects. In essence, angular acceleration provides a deeper layer of insight into the complexities of rotational dynamics.
Real-world Applications:
The applications of angular acceleration are vast and diverse. Consider a car turning a corner – the change in its angular velocity is a result of angular acceleration. This concept is also fundamental in the design and analysis of machinery, such as the rotating components of engines or the motion of a gyroscope.

Kinematics Equation of Rotational Motion:
In the realm of rotational motion, kinematics equations describe the relationships between various rotational parameters without considering the forces causing the motion. These equations parallel their linear motion counterparts but involve angular quantities. Here are some fundamental kinematics equations for rotational motion:

This equation connects final angular velocity (ω) to initial angular velocity (w0), angular acceleration (α), and angular displacement (θ).
These kinematics equations for rotational motion offer a comprehensive framework for analysing the motion of objects undergoing rotation. They serve as powerful tools in solving problems related to rotating systems, providing a bridge between angular displacement, velocity, acceleration, and time. Understanding and applying these equations contribute significantly to unravelling the complexities of rotational dynamics.
CBSE Class 11th Downloadable Resources:
| 1. CBSE Class 11th Topic Wise Summary | View Page / Download |
| 2. CBSE Class 11th NCERT Books | View Page / Download |
| 3. CBSE Class 11th NCERT Solutions | View Page / Download |
| 4. CBSE Class 11th Exemplar | View Page / Download |
| 5. CBSE Class 11th Sample Papers | View Page / Download |
| 6. CBSE Class 11th Question Bank | View Page / Download |
| 7. CBSE Class 11th Topic Wise Revision Notes | View Page / Download |
| 8. CBSE Class 11th Last Minutes Preparation Resources | View Page / Download |
| 9. CBSE Class 11th Best Reference Books | View Page / Download |
| 10. CBSE Class 11th Formula Booklet | View Page / Download |
Being in CBSE class 11th and considering the board examinations you must be needing resources to excel in your examinations. At TestprepKart we take great pride in providing CBSE class 11th all study resources in downloadable form for you to keep you going.
Below is the list of all CBSE class 11th Downloads available on TestprepKart for both Indian and NRI students preparing for CBSE class 11th in UAE, Oman, Qatar, Kuwait & Bahrain.
SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES:
Q1. What is rotational motion about a fixed axis?
Answer 1. Rotational motion about a fixed axis occurs when an object rotates around an axis without changing its orientation. The axis remains stationary during the rotation.
Q2. What is angular displacement in rotational motion?
Answer 2. Angular displacement (θ) is the measure of how much an object has rotated about a fixed axis. It is usually measured in radians and can be positive or negative, depending on the direction of rotation.
Q3. How is angular velocity defined in rotational motion?
Answer 3. Angular velocity (ω) is the rate at which an object rotates about a fixed axis. It is the time derivative of angular displacement (θ) and is measured in radians per second (rad/s).
Q4. What is the relationship between linear and angular velocity?
Answer 4. Linear velocity (v) is related to angular velocity (ω) by the formula v=r⋅ω, where r is the distance from the axis of rotation to the point of interest.
Q5. How does angular acceleration influence rotational motion?
Answer 5. Angular acceleration (α) represents the rate at which angular velocity changes with time. It is related to changes in rotational speed and is crucial in describing the dynamics of rotating systems.
Leave a Reply