In the captivating world of physics, the study of rotational motion about a fixed axis unravels a mesmerising dance of forces, torques, and dynamic equilibrium. This exploration delves into the intricate dynamics governing the rotation of objects around a stationary axis, offering a profound understanding of angular displacement, velocity, and acceleration.
Unravelling the Intricacies: Exploring the Dynamics of Rotational Motion Around a Fixed Axis
At the heart of this study lies the concept of a fixed axis, an imaginary line around which an object rotates without altering its orientation. Whether it's the turning of a wheel, the spinning of celestial bodies, or the gyration of a dancer, the fixed axis serves as a central reference point for analysing rotational dynamics.
What is Rotational Motion?
Rotational motion is a fundamental aspect of physics, depicting the motion of an object as it spins or revolves around a fixed point, known as an axis. In this dynamic dance, objects undergo circular or rotational motion, introducing a new set of parameters distinct from linear motion.
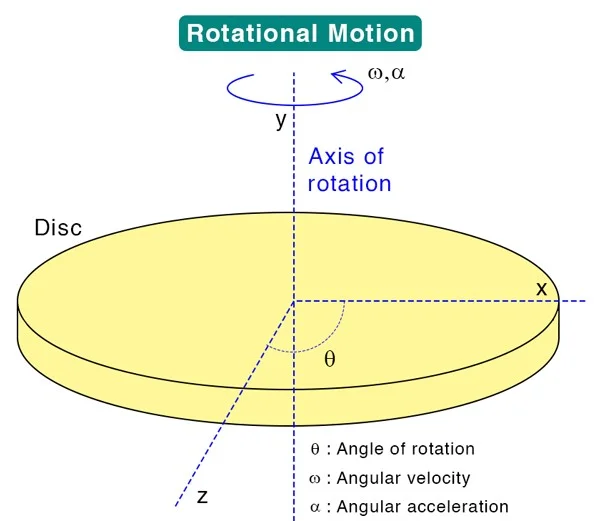
Key Components of Rotational Motion:
Angular Displacement:
-
Angular displacement measures how far an object has rotated around an axis. It is analogous to linear displacement but is expressed in terms of angles, often measured in radians.
Angular Velocity:
-
Angular velocity denotes the rate at which an object rotates around an axis. It describes how quickly the angular displacement changes with time, with units typically in radians per second.
Angular Acceleration:
-
Angular acceleration represents the rate at which angular velocity changes. It provides insight into the object's rotational acceleration or deceleration.
Rotational Motion About a Fixed Axis:
Rotational motion about a fixed axis is a captivating spectacle in the realm of physics, depicting the intricate dance of objects as they twirl or spin around an unchanging point. This specialised form of motion introduces a set of principles and phenomena that govern rotational dynamics, offering a unique perspective distinct from linear motion.
Key Concepts in Rotational Motion About a Fixed Axis:
Fixed Axis Defined:
-
At the core of this study is the notion of a fixed axis—an imaginary line around which an object rotates without altering its orientation. This axis serves as the anchor, providing a stable reference point for analysing the complex dynamics of rotation.
Angular Displacement:
-
Angular displacement measures the extent to which an object has rotated about the fixed axis. It quantifies the angle through which the object has turned and forms the foundational parameter for understanding rotational motion.
Angular Velocity:
-
Angular velocity enters the stage, describing the speed at which an object rotates about the fixed axis. It illustrates how rapidly the angular displacement changes over time, with units typically measured in radians per second.
Angular Acceleration:
-
Angular acceleration steps in to reveal the rate at which the angular velocity evolves. It elucidates whether the rotational speed is accelerating or decelerating, contributing to the dynamic behaviour of rotating systems.
Rotational Motion Examples
Rotational motion is a prevalent phenomenon with numerous examples found in everyday life, nature, and various scientific disciplines. Here are some illustrative examples:
Spinning Tops:
-
Spinning tops demonstrate pure rotational motion, rotating about a fixed axis. The interaction between the spinning top and the surface creates intricate patterns, showcasing the dynamics of rotational motion.
Rotating Wheels:
-
The wheels of vehicles, such as cars, bicycles, and rollerblades, undergo rotational motion as they spin around their axles. Understanding rotational dynamics is crucial for designing efficient and stable wheel systems.
Ceiling Fans:
-
The blades of a ceiling fan rotate about a fixed axis, producing air circulation. The speed and direction of rotation are controlled to regulate air movement in a room.
Earth's Rotation:
-
The Earth exhibits rotational motion about its axis, causing day and night cycles. This natural example illustrates the vast scale at which rotational motion occurs in celestial bodies.
Record Player Turntable:
-
A record player turntable exemplifies rotational motion as it spins the vinyl record. The needle reads the grooves on the rotating record, converting the information into sound.

Rotational Motion Dynamics
Rotational motion dynamics delves into the intricate forces, torques, and principles governing the rotational behaviour of objects around a fixed axis. This captivating field expands upon the fundamental concepts of angular displacement, velocity, and acceleration, offering a profound understanding of the underlying forces shaping the dynamic world of rotation.
1. Torque – The Rotational Force:
-
Torque is the driving force behind rotational motion, analogous to force in linear motion.It is calculated as the product of the force applied and the lever arm's distance from the axis of rotation.Torque induces angular acceleration, influencing how rapidly an object rotates.
2. Angular Acceleration – Dynamic Twists:
-
Angular acceleration (α) represents the rate of change of angular velocity with respect to time.It is influenced by the net torque acting on an object and its moment of inertia.The equationτ=I⋅α relates torque (τ) to angular acceleration and moment of inertia (I).
3. Moment of Inertia – Rotational Resistance:
-
Moment of inertia (I) quantifies an object's resistance to changes in its rotation.It depends on both mass distribution and the axis of rotation.The parallel axis theorem aids in calculating moment of inertia for axes parallel to an object's centre of mass.
4. Conservation of Angular Momentum:
-
Angular momentum (L) is conserved in the absence of external torques.The product of moment of inertia and angular velocity remains constant. L=I⋅ω.This principle explains the graceful pirouettes of figure skaters when they pull in their arms, reducing moment of inertia and increasing angular velocity.
5. Rolling Motion:
-
Objects undergoing rolling motion experience a combination of translational and rotational dynamics.The relationship between linear velocity (v) and angular velocity (ω) is given by v=R⋅ω, where R is the radius.
Comparison of Translational Motion and Rotational Motion

CBSE Class 11th Downloadable Resources:
| 1. CBSE Class 11th Topic Wise Summary | View Page / Download |
| 2. CBSE Class 11th NCERT Books | View Page / Download |
| 3. CBSE Class 11th NCERT Solutions | View Page / Download |
| 4. CBSE Class 11th Exemplar | View Page / Download |
| 5. CBSE Class 11th Sample Papers | View Page / Download |
| 6. CBSE Class 11th Question Bank | View Page / Download |
| 7. CBSE Class 11th Topic Wise Revision Notes | View Page / Download |
| 8. CBSE Class 11th Last Minutes Preparation Resources | View Page / Download |
| 9. CBSE Class 11th Best Reference Books | View Page / Download |
| 10. CBSE Class 11th Formula Booklet | View Page / Download |
Being in CBSE class 11th and considering the board examinations you must be needing resources to excel in your examinations. At TestprepKart we take great pride in providing CBSE class 11th all study resources in downloadable form for you to keep you going.
Below is the list of all CBSE class 11th Downloads available on TestprepKart for both Indian and NRI students preparing for CBSE class 11th in UAE, Oman, Qatar, Kuwait & Bahrain.
SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES:
Q1. What is rotational motion about a fixed axis?
Answer: Rotational motion about a fixed axis refers to the spinning or rotation of an object around an axis that remains stationary during the motion. This axis serves as a fixed reference point.
Q2. How is angular displacement different from linear displacement?
Answer: Angular displacement (θ) measures the extent of rotation in radians, while linear displacement measures the change in position along a straight line.
Q3. What role does torque play in rotational motion?
Answer: Torque is the rotational analog of force and causes angular acceleration. It is essential in understanding the dynamics of rotational motion and is calculated as the product of force and lever arm distance.
Q4. How is angular velocity related to linear velocity?
Answer: The relationship between angular velocity (ω) and linear velocity (v) is given by v=r⋅ω, where r is the distance from the axis of rotation to the point of interest.
Q5. What factors influence the moment of inertia of an object?
Answer: Moment of inertia depends on the mass distribution of an object and its axis of rotation. Objects with mass concentrated farther from the axis have larger moments of inertia.
Leave a Reply