In the vast world of mathematics, certain principles serve as the foundation for understanding and unraveling its intricacies. One such fundamental concept that holds immense significance is the "Fundamental Theorem of Arithmetic.
Decoding the Mathematical Marvels CBSE Class 10 NCERT Mathematics Unveiling The Fundamental Theorem Of Arithmetic

This theorem, often regarded as a cornerstone in number theory, plays a pivotal role in comprehending the unique nature of integers and their prime factorization.
Understanding the Basics
Before delving into the theorem itself, let's revisit some essential concepts. In the realm of integers, numbers that can be expressed as the product of prime numbers are particularly fascinating. This process is known as prime factorization, and it forms the basis for the Fundamental Theorem of Arithmetic.
The Fundamental Theorem Unveiled

The Fundamental Theorem of Arithmetic, a jewel in the crown of number theory, states that every positive integer greater than 1 can be uniquely expressed as the product of prime numbers. This theorem emphasizes the idea that the prime factorization of a number is essentially its mathematical DNA.
Uniqueness Matters

One of the key aspects of the Fundamental Theorem is the uniqueness of prime factorization. It asserts that although there may be multiple ways to arrive at a number's prime factorization, the actual primes involved in the decomposition are unique. This characteristic distinguishes the theorem from mere factorization and underscores the beauty and order inherent in the world of integers.
Q1 Fundamental Theorem of Arithmetic ExamplesExample Question: In a formula racing competition the time taken by two racing cars A and B to complete 1 round of the track is 30 minutes and 45 minutes respectively. After how much time will the cars meet again at the starting point?
Solution As the time taken by car B is more compared to that of A to complete one round it can be assumed that A will reach early and both the cars will meet again when A has already reached the starting point. This time can be calculated by finding the L.C.M of the time taken by each.
30 = 2 × 3 × 5
45 = 3 × 3 × 5
The L.C.M is 90.
Key Concepts for Class 10 CBSE
Prime Factorization: The process of expressing a number as the product of its prime factors.
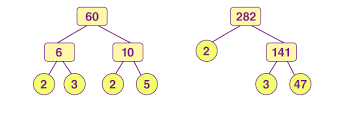
Uniqueness of Prime Factorization: Emphasising the distinctiveness of prime factorization for each positive integer.
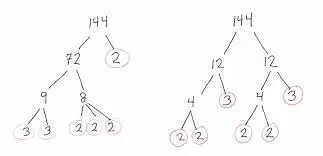
CBSE Class 10th Downloadable Resources:
| 1. CBSE Class 10th Topic Wise Summary | View Page / Download |
| 2. CBSE Class 10th NCERT Books | View Page / Download |
| 3. CBSE Class 10th NCERT Solutions | View Page / Download |
| 4. CBSE Class 10th Exemplar | View Page / Download |
| 5. CBSE Class 10th Previous Year Papers | View Page / Download |
| 6. CBSE Class 10th Sample Papers | View Page / Download |
| 7. CBSE Class 10th Question Bank | View Page / Download |
| 8. CBSE Class 10th Topic Wise Revision Notes | View Page / Download |
| 9. CBSE Class 10th Last Minutes Preparation Resources (LMP) | View Page / Download |
| 10. CBSE Class 10th Best Reference Books | View Page / Download |
| 11. CBSE Class 10th Formula Booklet | View Page / Download |
Being in CBSE class 10th and considering the board examinations you must be needing resources to excel in your examinations. At TestprepKart we take great pride in providing CBSE class 10th all study resources in downloadable form for you to keep you going.
Below is the list of all CBSE class 10th Downloads available on TestprepKart for both Indian and NRI students preparing for CBSE class 10th in UAE, Oman, Qatar, Kuwait & Bahrain.
FAQ
Q1: What is the Fundamental Theorem of Arithmetic?
Ans: The Fundamental Theorem of Arithmetic states that every positive integer greater than 1 can be expressed uniquely as a product of prime numbers.
Q2: Why is the uniqueness part crucial in the Fundamental Theorem of Arithmetic?
Ans: Uniqueness ensures that there is only one way to decompose a given number into prime factors, providing a distinct factorization for each positive integer.
Q3: Can you provide an example illustrating the Fundamental Theorem of Arithmetic?
Ans: Certainly! For example, the number 84 can be expressed as the product of primes:
22×3×7
Q4: What role do prime numbers play in the Fundamental Theorem of Arithmetic?
Ans: Prime numbers serve as the building blocks, as every composite number can be decomposed into a unique combination of prime factors.
Q5: How does the Fundamental Theorem impact number theory and mathematical reasoning?
Ans: It forms the basis for number theory, enabling mathematicians to explore the properties of numbers and understand the relationships between them.

Leave a Reply