In the intricate tapestry of physics and engineering, the concept of equilibrium emerges as a guiding principle that governs the stability and balance of rigid bodies. Whether we are contemplating the majestic architecture of a bridge, the nimble movements of an athlete, or the complexities of a machine in motion, understanding the equilibrium of a rigid body unveils the art of achieving harmony amid external forces and torques.
Mastering Balance: Exploring the Art and Science of Equilibrium in Rigid Bodies
What Do You Mean by Equilibrium of Rigid Body?
The equilibrium of a rigid body refers to a state in which the body is either at rest or moving at a constant velocity, and there is no net force or torque acting on it. In other words, the forces and torques acting on the rigid body are balanced, leading to a condition where there is no linear acceleration or angular acceleration.
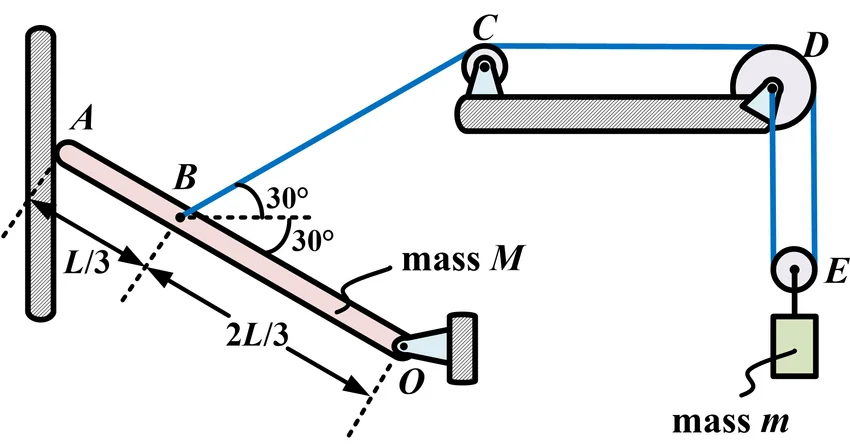
To understand this concept, let's break it down into two main components:
Translational Equilibrium:
For a rigid body to be in translational equilibrium, the vector sum of all external forces acting on it must be zero.
Mathematically, this condition is expressed as:
-
ΣF=0.
This ensures that the body is not accelerating in any linear direction; it is either at rest or moving with a constant velocity.
Rotational Equilibrium:
Achieving rotational equilibrium involves ensuring that the sum of all external torques (moments) acting on the rigid body is zero.
Mathematically, this condition is expressed as:
-
Στ=0.
This ensures that the body is not undergoing angular acceleration or rotation.
The combined satisfaction of both translational and rotational equilibrium conditions means that the rigid body is in complete equilibrium. It can be a powerful concept in understanding and predicting the behaviour of structures, objects, and systems subjected to external forces.
Rigid Body in Motion
A rigid body in motion is a physical object that maintains its shape and does not deform while undergoing either translational or rotational motion, or a combination of both. Understanding the motion of a rigid body is crucial in physics and engineering, as it involves concepts such as linear and angular motion, velocity, acceleration, and momentum.
Translational Motion:
Linear Motion:
In translational motion, a rigid body experiences a change in position without any internal deformation.
Equations of Motion: The kinematic equations for linear motion, such as
s=ut+1/2at2
s=ut+ , describe the displacement (s), initial velocity (u), acceleration (a), and time (t) relationships.
Velocity and Acceleration:
The velocity of a rigid body in translational motion is the rate of change of its displacement with respect to time.
Acceleration is the rate of change of velocity and can result from external forces acting on the body.

Rotational Motion:
Angular Motion:
A rigid body can undergo rotational motion, where it rotates about a fixed axis.
Angular Displacement: Describes the angle through which the body rotates.
Angular Velocity and Acceleration: Represent the rate of change of angular displacement and velocity.
Torque and Moment of Inertia:
Torque (τ) is the rotational equivalent of force, causing angular acceleration.
Moment of inertia (I) quantifies the body's resistance to changes in rotational motion.
Combined Motion:
General Motion:
A rigid body can experience both translational and rotational motion simultaneously.
The motion of each particle within the body contributes to its overall motion.
Center of Mass:
The centre of mass of a rigid body is a point that moves as if all the mass were concentrated at that point during translational motion.
Center of Gravity
The centre of gravity (CG) is a crucial concept in physics and engineering, representing the point where the entire weight of an object can be considered to act. It is the average location of the gravitational force acting on the individual particles that make up an object. The centre of gravity is a key parameter in understanding the stability and equilibrium of objects subjected to external forces. Here are key points about the centre of gravity:
Definition:
-
The centre of gravity is the point where the entire weight of an object can be concentrated, and the gravitational force can be considered to act. In uniform gravitational fields, the centre of gravity coincides with the centre of mass.
Center of Mass vs. Center of Gravity:
-
While the terms are often used interchangeably, the centre of mass (COM) refers to the average position of mass in an object, while the centre of gravity specifically considers the distribution of weight due to gravitational forces.
Location:
-
The location of the centre of gravity depends on the distribution of mass within an object. In symmetrical and uniform objects, the centre of gravity is at the geometric centre. However, irregular shapes or varying densities can result in an offset centre of gravity.
Effects on Stability:
-
The stability of an object is influenced by the position of its centre of gravity. An object is stable if its centre of gravity is located over its base of support. In contrast, an object may tip or topple if its centre of gravity falls outside its base.
Calculation:
-
For simple and symmetric objects, the centre of gravity can be calculated using geometric considerations. In more complex cases, numerical methods or experimental measurements may be employed.
SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES:
Q1 What is the equilibrium of a rigid body?
Answer: Equilibrium of a rigid body refers to a state where the body is either at rest or moving at a constant velocity, with no net force or torque acting on it.
Q2 Why is equilibrium important in physics and engineering?
Answer: Equilibrium is crucial for analysing and designing structures, machines, and systems to ensure stability, safety, and efficient operation.
Q3 What are the conditions for translational equilibrium?
Answer: Translational equilibrium requires that the vector sum of all external forces acting on the body is zero:
Q4 Explain rotational equilibrium.
Answer: Rotational equilibrium requires that the sum of all external torques acting on the body is zero:
Στ=0. It ensures the body does not undergo angular acceleration.
Q5 Can a rigid body be in equilibrium while in motion?
Answer: Yes, a rigid body can be in equilibrium while in constant velocity motion. It satisfies both translational and rotational equilibrium conditions.

Leave a Reply